Adversarial Search & Constraint Satisfaction Problems

Soal :

1. Apa yang dimaksud Adversarial Search & Constraint Satisfaction Problems ? berikan contoh ?
2. Apa itu Propositional Logic ? berikan contoh ?
3. Buat coding (Boleh C, C++ atau Java) untuk  Algoritma A & Algoritma A* (A Star )?

Jawaban :

1.  – Adversarial Search :

Algoritma pencarian yang memeriksa masalah yang timbul ketika kita mencoba untuk merencanakan suatu langkah ke depan tetapi ada agen-agen lain berencana melawan kita.

atau

Algoritma pencarian yang digunakan dalam permainan di mana satu pemain mencoba untuk memaksimalkan nilai mereka (menang) tetapi ditentang oleh pemain lain ( AI, Player Computer ).

biasa digunakan untuk pencarian dalam game ( Catur, Tic Tac Toe, dll.)

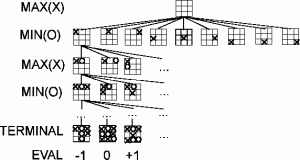
Algoritma yang biasa digunakan : MiniMax, Alpha–beta pruning.

Gambar Algoritma Minimax :

– Constraint Satisfaction Problems :

Sebuah pendekatan dari problem yang bersifat matematis dengan tujuan menemukan keadaan atau obyek yang memenuhi sejumlah persyaratan atau kiteria. Sebuah Constraint diartikan sebagai batasan solusi memungkinkan dalam sebuah problem optimasi.

Singkatnya menyelesaikan masalah dengan pemenuhan batasan.

Contoh masalah sederhana yang dapat dimodelkan dengan CSP :

• Eight queens puzzle
• Map coloring problem
• Sudoku, Futoshiki, Kakuro (Cross Sums), Numbrix, Hidato and many other logic puzzles.

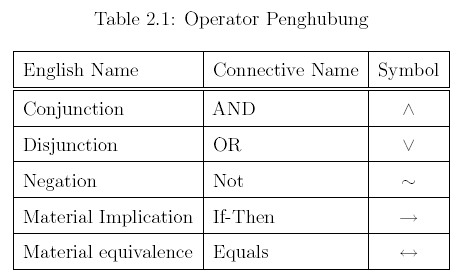
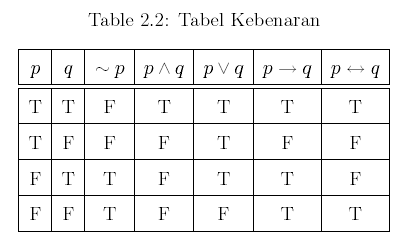
2.    Propositional logic merupakan salah satu bentuk (bahasa) representasi logika yang paling tua dan paling sederhana. Dengan cara ini beberapa fakta dapat digambarkan dan dimanipulasi dengan menggunakan aturan-aturan aljabar Boolean.

Contoh :

Jika seseorang itu adalah mahasiswa maka ia pasti pandai

Dian Sastro adalah seorang mahasiswa

——————————————————————————–

Dian Sastro pasti pandai

p = mahasiswa

q = pandai

p -> q

p

———

 q

3.    – Best – First / Algoritma A :

[code language=”css”]
import java.util.Comparator;

import java.util.InputMismatchException;

import java.util.PriorityQueue;

import java.util.Scanner;

public class BestFirstSearch

{

private PriorityQueue<Vertex> priorityQueue;

private int heuristicvalues[];

private int numberOfNodes;

public static final int MAX_VALUE = 999;

public BestFirstSearch(int numberOfNodes)

{

this.numberOfNodes = numberOfNodes;

this.priorityQueue = new PriorityQueue<Vertex>(this.numberOfNodes,

new Vertex());

}

public void bestFirstSearch(int adjacencyMatrix[][], int[] heuristicvalues,int source)

{

int evaluationNode;

int destinationNode;

int visited[] = new int [numberOfNodes + 1];

this.heuristicvalues = heuristicvalues;

priorityQueue.add(new Vertex(source, this.heuristicvalues[source]));

visited[source] = 1;

while (!priorityQueue.isEmpty())

{

evaluationNode = getNodeWithMinimumHeuristicValue();

destinationNode = 1;

System.out.print(evaluationNode + "\t");

while (destinationNode <= numberOfNodes)

{

Vertex vertex = new Vertex(destinationNode,this.heuristicvalues[destinationNode]);

if ((adjacencyMatrix[evaluationNode][destinationNode] != MAX_VALUE

&& evaluationNode != destinationNode)&& visited[destinationNode] == 0)

{

priorityQueue.add(vertex);

visited[destinationNode] = 1;

}

destinationNode++;

}

}

}

private int getNodeWithMinimumHeuristicValue()

{

Vertex vertex = priorityQueue.remove();

return vertex.node;

}

public static void main(String… arg)

{

int adjacency_matrix[][];

int number_of_vertices;

int source = 0;

int heuristicvalues[];

Scanner scan = new Scanner(System.in);

try

{

System.out.println("Enter the number of vertices");

number_of_vertices = scan.nextInt();

adjacency_matrix = new int[number_of_vertices + 1][number_of_vertices + 1];

heuristicvalues = new int[number_of_vertices + 1];

System.out.println("Enter the Weighted Matrix for the graph");

for (int i = 1; i <= number_of_vertices; i++)

{

for (int j = 1; j <= number_of_vertices; j++)

{

adjacency_matrix[i][j] = scan.nextInt();

if (i == j)

{

adjacency_matrix[i][j] = 0;

continue;

}

if (adjacency_matrix[i][j] == 0)

{

adjacency_matrix[i][j] = MAX_VALUE;

}

}

}

for (int i = 1; i <= number_of_vertices; i++)

{

for (int j = 1; j <= number_of_vertices; j++)

{

if (adjacency_matrix[i][j] == 1 && adjacency_matrix[j][i] == 0)

{

adjacency_matrix[j][i] = 1;

}

}

}

System.out.println("Enter the heuristic values of the nodes");

for (int vertex = 1; vertex <= number_of_vertices; vertex++)

{

System.out.print(vertex + ".");

heuristicvalues[vertex] = scan.nextInt();

System.out.println();

}

System.out.println("Enter the source ");

source = scan.nextInt();

System.out.println("The graph is explored as follows");

BestFirstSearch bestFirstSearch = new BestFirstSearch(number_of_vertices);

bestFirstSearch.bestFirstSearch(adjacency_matrix, heuristicvalues,source);

} catch (InputMismatchException inputMismatch)

{

System.out.println("Wrong Input Format");

}

scan.close();

}

}

class Vertex implements Comparator<Vertex>

{

public int heuristicvalue;

public int node;

public Vertex(int node, int heuristicvalue)

{

this.heuristicvalue = heuristicvalue;

this.node = node;

}

public Vertex()

{

}

@Override

public int compare(Vertex vertex1, Vertex vertex2)

{

if (vertex1.heuristicvalue < vertex2.heuristicvalue)

return -1;

if (vertex1.heuristicvalue > vertex2.heuristicvalue)

return 1;

return 0;

}

@Override

public boolean equals(Object obj)

{

if (obj instanceof Vertex)

{

Vertex node = (Vertex) obj;

if (this.node == node.node)

{

return true;

}

}

return false;

}

}
[/code]

– Algoritma A* :

[code language=”css”]
// Astar.cpp
// http://en.wikipedia.org/wiki/A*
// Compiler: Dev-C++ 4.9.9.2
// FB – 201012256
#include <iostream>
#include <iomanip>
#include <queue>
#include <string>
#include <math.h>
#include <ctime>
using namespace std;

const int n=60; // horizontal size of the map
const int m=60; // vertical size size of the map
static int map[n][m];
static int closed_nodes_map[n][m]; // map of closed (tried-out) nodes
static int open_nodes_map[n][m]; // map of open (not-yet-tried) nodes
static int dir_map[n][m]; // map of directions
const int dir=8; // number of possible directions to go at any position
// if dir==4
//static int dx[dir]={1, 0, -1, 0};
//static int dy[dir]={0, 1, 0, -1};
// if dir==8
static int dx[dir]={1, 1, 0, -1, -1, -1, 0, 1};
static int dy[dir]={0, 1, 1, 1, 0, -1, -1, -1};

class node
{
// current position
int xPos;
int yPos;
// total distance already travelled to reach the node
int level;
// priority=level+remaining distance estimate
int priority; // smaller: higher priority

public:
node(int xp, int yp, int d, int p)
{xPos=xp; yPos=yp; level=d; priority=p;}

int getxPos() const {return xPos;}
int getyPos() const {return yPos;}
int getLevel() const {return level;}
int getPriority() const {return priority;}

void updatePriority(const int & xDest, const int & yDest)
{
priority=level+estimate(xDest, yDest)*10; //A*
}

// give better priority to going strait instead of diagonally
void nextLevel(const int & i) // i: direction
{
level+=(dir==8?(i%2==0?10:14):10);
}

// Estimation function for the remaining distance to the goal.
const int & estimate(const int & xDest, const int & yDest) const
{
static int xd, yd, d;
xd=xDest-xPos;
yd=yDest-yPos;

// Euclidian Distance
d=static_cast<int>(sqrt(xd*xd+yd*yd));

// Manhattan distance
//d=abs(xd)+abs(yd);

// Chebyshev distance
//d=max(abs(xd), abs(yd));

return(d);
}
};

// Determine priority (in the priority queue)
bool operator<(const node & a, const node & b)
{
return a.getPriority() > b.getPriority();
}

// A-star algorithm.
// The route returned is a string of direction digits.
string pathFind( const int & xStart, const int & yStart,
const int & xFinish, const int & yFinish )
{
static priority_queue<node> pq[2]; // list of open (not-yet-tried) nodes
static int pqi; // pq index
static node* n0;
static node* m0;
static int i, j, x, y, xdx, ydy;
static char c;
pqi=0;

// reset the node maps
for(y=0;y<m;y++)
{
for(x=0;x<n;x++)
{
closed_nodes_map[x][y]=0;
open_nodes_map[x][y]=0;
}
}

// create the start node and push into list of open nodes
n0=new node(xStart, yStart, 0, 0);
n0->updatePriority(xFinish, yFinish);
pq[pqi].push(*n0);
open_nodes_map[x][y]=n0->getPriority(); // mark it on the open nodes map

// A* search
while(!pq[pqi].empty())
{
// get the current node w/ the highest priority
// from the list of open nodes
n0=new node( pq[pqi].top().getxPos(), pq[pqi].top().getyPos(),
pq[pqi].top().getLevel(), pq[pqi].top().getPriority());

x=n0->getxPos(); y=n0->getyPos();

pq[pqi].pop(); // remove the node from the open list
open_nodes_map[x][y]=0;
// mark it on the closed nodes map
closed_nodes_map[x][y]=1;

// quit searching when the goal state is reached
//if((*n0).estimate(xFinish, yFinish) == 0)
if(x==xFinish && y==yFinish)
{
// generate the path from finish to start
// by following the directions
string path="";
while(!(x==xStart && y==yStart))
{
j=dir_map[x][y];
c=’0’+(j+dir/2)%dir;
path=c+path;
x+=dx[j];
y+=dy[j];
}

// garbage collection
delete n0;
// empty the leftover nodes
while(!pq[pqi].empty()) pq[pqi].pop();
return path;
}

// generate moves (child nodes) in all possible directions
for(i=0;i<dir;i++)
{
xdx=x+dx[i]; ydy=y+dy[i];

if(!(xdx<0 || xdx>n-1 || ydy<0 || ydy>m-1 || map[xdx][ydy]==1
|| closed_nodes_map[xdx][ydy]==1))
{
// generate a child node
m0=new node( xdx, ydy, n0->getLevel(),
n0->getPriority());
m0->nextLevel(i);
m0->updatePriority(xFinish, yFinish);

// if it is not in the open list then add into that
if(open_nodes_map[xdx][ydy]==0)
{
open_nodes_map[xdx][ydy]=m0->getPriority();
pq[pqi].push(*m0);
// mark its parent node direction
dir_map[xdx][ydy]=(i+dir/2)%dir;
}
else if(open_nodes_map[xdx][ydy]>m0->getPriority())
{
// update the priority info
open_nodes_map[xdx][ydy]=m0->getPriority();
// update the parent direction info
dir_map[xdx][ydy]=(i+dir/2)%dir;

// replace the node
// by emptying one pq to the other one
// except the node to be replaced will be ignored
// and the new node will be pushed in instead
while(!(pq[pqi].top().getxPos()==xdx &&
pq[pqi].top().getyPos()==ydy))
{
pq[1-pqi].push(pq[pqi].top());
pq[pqi].pop();
}
pq[pqi].pop(); // remove the wanted node

// empty the larger size pq to the smaller one
if(pq[pqi].size()>pq[1-pqi].size()) pqi=1-pqi;
while(!pq[pqi].empty())
{
pq[1-pqi].push(pq[pqi].top());
pq[pqi].pop();
}
pqi=1-pqi;
pq[pqi].push(*m0); // add the better node instead
}
else delete m0; // garbage collection
}
}
delete n0; // garbage collection
}
return ""; // no route found
}

int main()
{
srand(time(NULL));

// create empty map
for(int y=0;y<m;y++)
{
for(int x=0;x<n;x++) map[x][y]=0;
}

// fillout the map matrix with a ‘+’ pattern
for(int x=n/8;x<n*7/8;x++)
{
map[x][m/2]=1;
}
for(int y=m/8;y<m*7/8;y++)
{
map[n/2][y]=1;
}

// randomly select start and finish locations
int xA, yA, xB, yB;
switch(rand()%8)
{
case 0: xA=0;yA=0;xB=n-1;yB=m-1; break;
case 1: xA=0;yA=m-1;xB=n-1;yB=0; break;
case 2: xA=n/2-1;yA=m/2-1;xB=n/2+1;yB=m/2+1; break;
case 3: xA=n/2-1;yA=m/2+1;xB=n/2+1;yB=m/2-1; break;
case 4: xA=n/2-1;yA=0;xB=n/2+1;yB=m-1; break;
case 5: xA=n/2+1;yA=m-1;xB=n/2-1;yB=0; break;
case 6: xA=0;yA=m/2-1;xB=n-1;yB=m/2+1; break;
case 7: xA=n-1;yA=m/2+1;xB=0;yB=m/2-1; break;
}

cout<<"Map Size (X,Y): "<<n<<","<<m<<endl;
cout<<"Start: "<<xA<<","<<yA<<endl;
cout<<"Finish: "<<xB<<","<<yB<<endl;
// get the route
clock_t start = clock();
string route=pathFind(xA, yA, xB, yB);
if(route=="") cout<<"An empty route generated!"<<endl;
clock_t end = clock();
double time_elapsed = double(end – start);
cout<<"Time to calculate the route (ms): "<<time_elapsed<<endl;
cout<<"Route:"<<endl;
cout<<route<<endl<<endl;

// follow the route on the map and display it
if(route.length()>0)
{
int j; char c;
int x=xA;
int y=yA;
map[x][y]=2;
for(int i=0;i<route.length();i++)
{
c =route.at(i);
j=atoi(&c);
x=x+dx[j];
y=y+dy[j];
map[x][y]=3;
}
map[x][y]=4;

// display the map with the route
for(int y=0;y<m;y++)
{
for(int x=0;x<n;x++)
if(map[x][y]==0)
cout<<".";
else if(map[x][y]==1)
cout<<"O"; //obstacle
else if(map[x][y]==2)
cout<<"S"; //start
else if(map[x][y]==3)
cout<<"R"; //route
else if(map[x][y]==4)
cout<<"F"; //finish
cout<<endl;
}
}
getchar(); // wait for a (Enter) keypress
return(0);
}

[/code]